Exponentialfunktion
Die Exponentialfunktion ist die Grundlage aller Prozesse, bei denen sich ein Wert in konstanten Schritten vervielfacht – sei es das Wachstum von Bakterienkulturen, das Zinseszinsprinzip oder die Ausbreitung von Informationen im Internet. In ihrer allgemeinsten Form lautet sie
\[ f(x) = a \cdot b^x \]wobei
- \(a\) den Startwert (den Funktionswert bei \(x=0\)) bestimmt,
- \(b\) die Basis ist, die angibt, um welchen Faktor sich der Funktionswert pro Einheit von \(x\) erhöht oder verringert, und
- \(x\) die unabhängige Variable (oft Zeit, aber auch andere Dimensionen).
Vergleich zwischen linearem und exponentiellem Wachstum
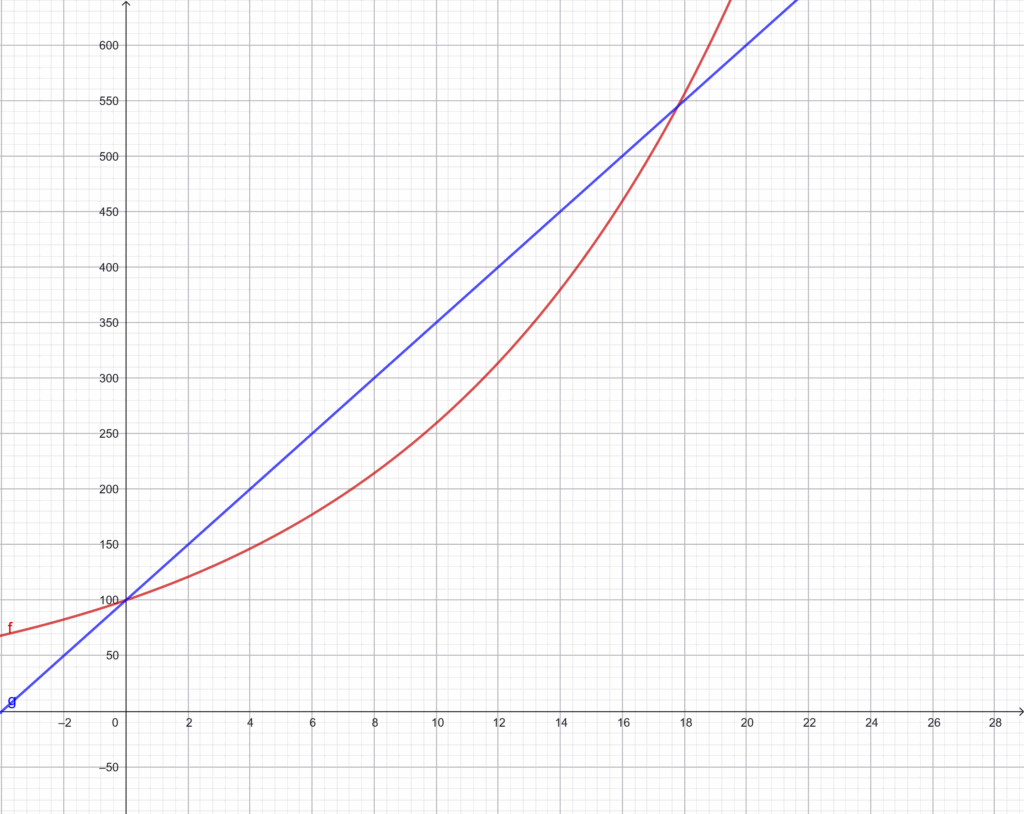
Im Gegensatz zum linearen Wachstum, bei dem die Zunahme konstant ist (z. B. \(g(x)=c \cdot x + d\)), wächst bei der Exponentialfunktion der Funktionswert mit zunehmendem \(x\) immer schneller – das „Wachstum beschleunigt sich“. Hierzu ein Beispiel: Wir vergleichen zwei sehr unterschiedliche Sparstrategien:
- Konto \(f\) erhält jeden Monat 10 % Zinsen auf den aktuellen Kontostand – das Wachstum ist exponentiell, weil die Zinsen selbst immer größer werden.
- Konto \(g\) bekommt jeden Monat eine feste Einzahlung von 25 € – das Wachstum ist linear, weil der Zuwachs konstant bleibt.
- Beide Konten starten mit 100 €.
| Monat \(t\) | Konto \(f\) | Konto \(g\) |
|---|---|---|
| 0 | € 100,00 | € 100,00 |
| 1 | € 110,00 | € 125,00 |
| 2 | € 121,00 | € 150,00 |
| … | … | … |
| 17 | € 505,43 | € 525,00 |
| 18 | € 555,97 | € 550,00 |
Zunächst wirkt das lineare Wachstum des Kontos \(g\) vielversprechend, weil das Geld rasch ansteigt. Mit der Zeit wird jedoch deutlich, dass das exponentielle Wachstum des Kontos \(f\) – obwohl es anfangs langsamer voranschreitet – langfristig das lineare Wachstum übertrifft.