Durchschnittliche Änderungsrate
Stell dir vor, du beobachtest, wie sich ein Objekt bewegt, wie schnell ein Wasserstand steigt oder wie sich ein Preis im Laufe der Zeit verändert. In allen diesen Situationen gibt es einen gemeinsamen Nenner: die Geschwindigkeit, mit der etwas sich ändert. Die durchschnittliche Änderungsrate beschreibt genau dieses Konzept – sie quantifiziert, wie viel sich eine Größe im Durchschnitt pro Zeiteinheit, Raum oder einer anderen unabhängigen Variable ändert.
Was bedeutet „durchschnittlich“?
Wenn wir von einer durchschnittlichen Änderungsrate sprechen, nehmen wir an, dass wir die Änderung über einen bestimmten Abschnitt hinweg betrachten. Anstatt die exakte Momentänderung (wie schnell etwas zu einem bestimmten Zeitpunkt ist) zu messen, schauen wir uns an, wie viel sich am Anfang und am Ende eines Intervalls geändert hat und teilen das Ergebnis durch die Länge des Intervalls. Dadurch erhalten wir eine „Durchschnittsgeschwindigkeit“, die uns sagt, wie schnell sich die Größe im Mittel verändert hat.
Mathematischer Ausdruck
Für eine gegebene Funktion \(y=f(x)\) – wobei \(x\) die unabhängige Variable (z. B. Zeit oder Strecke) und \(y\) die abhängige Größe (z. B. Position oder Temperatur) ist – lautet die Formel für die durchschnittliche Änderungsrate:
\[ m = \frac{\Delta y}{\Delta x} = \frac{f(b)-f(a)}{b-a} \]Hier steht \(\Delta y\) für die Änderung der Größe und \(\Delta x\) für die Änderung der unabhängigen Variable. Der Bruch liefert uns einen Wert, der angibt, wie viel \(y\) sich im Durchschnitt pro Einheit von \(x\) ändert. Man spricht hierbei auch von einem Steigungsdreieck.
Rechenbeispiel:
Gegeben sei die Funktion \(f(x)=x^2\). Bestimme die durchschnittliche Änderungsrate im Intervall \( [1;2] \).
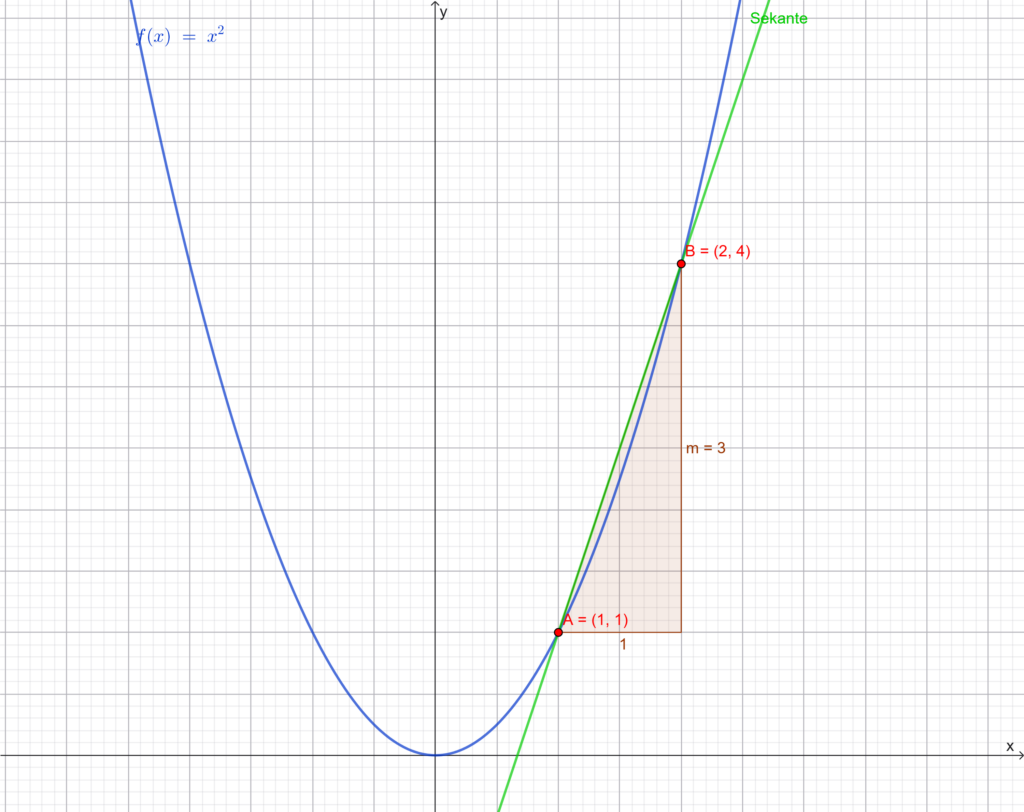
Da für die durschnittliche Änderungsrate
\[ m = \frac{f(b)-f(a)}{b-a} \]gilt, müssen wir zunächst
\[ f(a=1) = 1^2=1 \]und
\[ f(b=2) = 2^2=4 \]berechnen. Anschließend setzen wir diese Werte in die Formel für die durchschnittliche Änderungsrate ein:
\begin{align} m &= \frac{f(b)-f(a)}{b-a} \\ &= \frac{f(2)-f(1)}{2-1} \\ &= \frac{4-1}{2-1} \\ &= \frac{3}{1} \\ &= 3 \end{align}Somit ist die durschnittliche Änderungsrate \(m=3\).