Zahlenmengen
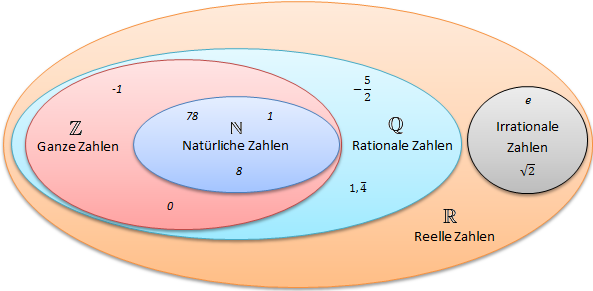
Zahlenmengen sind die Grundbausteine jeder mathematischen Arbeit. Sie gruppieren Zahlen nach gemeinsamen Eigenschaften und ermöglichen es dir, schnell zu erkennen, welche Operationen zulässig sind und welche nicht. In der Abbildung unten siehst du die wichtigsten Mengen – von den kleinsten bis zu den komplexesten – in einem übersichtlichem Venn‑Diagramm.
Kurzfassung
| Zahlenmenge | Kurz gesagt… |
|---|---|
| Natürliche Zahlen \(\mathbb{N}\) | „Nur positive ganze Zahlen“ – Zählen. Grundlage für Zählen, Indizierung, Primzahlen‑Analyse. |
| Ganze Zahlen \(\mathbb{Z}\) | „Alles, was du zählen kannst, plus die Gegenstücke“ – Addition, Subtraktion, Modulo. Erlaubt negative Werte, erlaubt die Definition von Modulo‑Operationen. |
| Rationale Zahlen \(\mathbb{Q}\) | „Alles, was du als Bruch schreiben kannst“ – rationale Approximationen. Erweitert \(\mathbb{Z}\) auf ein vollständig divisibles System, ermöglicht die Darstellung von Brüchen. |
| Reelle Zahlen \(\mathbb{R}\) | „Alles, was du auf der Zahlengerade siehst“ – stetige Größen. Vollständiges, dichte Zahlenfeld – notwendig für Analysis, Grenzwerte, stetige Funktionen. |
| Komplexe Zahlen \(\mathbb{C}\) | „Alles, was du brauchst, um jede Gleichung zu lösen“ – imaginäre Einheit, komplexe Analysis. Vollständiges algebraisches System – jede Polynomgleichung hat hier Lösungen. |
Natürliche Zahlen \(\mathbb{N}\)
| Merkmal | Detail |
|---|---|
| Definition | Die Menge aller positiven ganzen Zahlen. In manchen Lehrplänen wird \(0\) als natürliche Zahl betrachtet, in anderen beginnt \(\mathbb{N}\) bei \(1\). |
| Symbolische Darstellung | \(\mathbb{N}\) (oder \(\mathbb{N}_0\) für die Variante mit \(0\)) |
| Beispiele | \(1, 2, 3, 4, 5, … \) \(0\) (falls inkludiert) |
| Grundoperationen | Addition, Subtraktion (nur solange das Ergebnis noch \(\geq 1\) bzw. \(\geq 0\) bleibt), Multiplikation, Division (nur ganzzahlig) |
| Wichtige Eigenschaften | Monotonie: \(n<n+1\) für jedes \(n \in \mathbb{N}\). Keine negativen Elemente. Keine Brühelemente – also keine rationalen, irrationalen oder komplexen Komponenten. |
| Anwendungsgebiete | Zählen, Indizierung von Reihen, Definition von Induktion (Basisfall + Induktionsschritt). |
Ganze Zahlen \(\mathbb{Z}\)
| Merkmal | Detail |
|---|---|
| Definition | Alle natürlichen Zahlen, 0 und deren negativen Gegenstücke. Formal: \(\mathbb{Z}={…,−3,−2,−1,0,1,2,3,…}\). |
| Symbolische Darstellung | \(\mathbb{Z}\) |
| Beispiele | \(…, –5, –4, –3, –2, –1, 0, 1, 2, 3, 4, 5, …\) |
| Operationen | Addition/Subtraktion: Ergebnis bleibt immer in \(\mathbb{Z}\). Multiplikation: Ergebnis bleibt in \(\mathbb{Z}\). Division: Ergebnis ist nicht zwangsläufig in \(\mathbb{Z}\) (z. B. \(\frac{1}{2} \in \mathbb{Z}\)). |
| Besondere Eigenschaften | Gleichmäßig verteilt auf der Zahlengerade. Kein Komplement zu irrationalen Zahlen – sie sind nicht Teil von \(\mathbb{Z}\). |
| Anwendungsgebiete | Zählen von Gegenständen (mit Vorzeichen), Algebraische Gleichungen, Definition von Modulo‑Operationen. |
Rationale Zahlen \(\mathbb{Q}\)
| Merkmal | Detail |
|---|---|
| Definition | Alle Zahlen, die als Quotient zweier ganzer Zahlen dargestellt werden können, wobei der Nenner \(\neq 0\) ist. Formal: \(\mathbb{Q}={\frac{q}{p} \text{ mit } p,q \in \mathbb{Z} , q \neq 0}\). |
| Beispiele | \(\frac{1}{2}, −\frac{4}{7}, 3=\frac{3}{1}, 0=\frac{0}{1}, \frac{1}{3}, −\frac{9}{5}\) |
| Eigenschaften | Alle ganzen Zahlen sind rationale (z. B. \(5=\frac{5}{1}\)). Addition, Subtraktion, Multiplikation, und Division (außer durch 0) bleiben in \(\mathbb{Q}\). Jede rationale Zahl hat entweder einen endlichen oder periodischen Dezimalbruch (z. B. \(\frac{1}{3}=0,\overline{3}\)). |
| Besondere Operationen | Bruchgleichung:\(\frac{a}{b}=\frac{c}{d} \Leftrightarrow ad=bc\). Rechnen mit Dezimalbrüchen: Umwandlung in Brüche oder umgekehrt. |
| Anwendungsgebiete | Algebraische Gleichungen, Bruchrechnung, rationale Approximationen von reellen Zahlen. |
Irrationalen Zahlen
| Merkmal | Detail |
|---|---|
| Definition | Zahlen, die sich nicht als endlicher oder periodischer Dezimalbruch schreiben lassen. |
| Beispiele | \(\sqrt{2}, \pi, e, \ln{2}, \phi = \frac{1-\sqrt{5}}{2}\). |
| Eigenschaften | Unendliche, nicht‑periodische Dezimaldarstellung (z. B. \(1,41421356237…\)). Sie liegen zwischen rationalen Zahlen (z. B. \(\sqrt{2}\) liegt zwischen \(1\) und \(2\)). Im Gegensatz zu rationalen Zahlen haben sie keine exakte Bruchdarstellung. |
| Kategorien | Algebraisch: Wurzel aus einer ganzen Zahl, Lösungen von Polynomen mit ganzzahligen Koeffizienten (z. B. \(\sqrt{2}\)). Transzendent: Nicht algebraisch, z. B. \(\pi, e\). |
| Relation zu ℚ | Die Menge der Irrationalen ist unendlicher als die der Rationalen (unzählbar). Sie ergänzen \(\mathbb{Q}\) zu \(\mathbb{R}\) – zusammen bilden sie das vollständige, dichte Feld der reellen Zahlen. |
| Anwendungsgebiete | Physik (z. B. \(\pi\) in Kreisformeln), Mathematik (Transzendentalsätze), Ingenieurwesen (z. B. \(\sqrt{2}\) in Diagonalen). |
Warum passen die Irrationalen Zahlen nicht in die Menge der Rationalen Zahlen?
- Bruchform: Jede rationale Zahl ist ein Bruch, aber nicht jede reelle Zahl ist ein Bruch.
- Dezimaldarstellung: Rationale Zahlen haben endliche oder periodische Dezimalstellen; irrationale Zahlen haben unendliche, nicht‑periodische Stellen.
- Beispiel‑Check: \(\frac{3}{4}=0,75\) (rational). \(\sqrt{2}=1,4142135…\) (irrational – kein periodischer Bruch).
Kurz gesagt: Irrationale Zahlen sind die „geheimen” Reellen, die nicht in \(\frac{p}{q}\) passen. Sie sind unendlich, nicht periodisch und liegen zwischen rationalen Zahlen.
Reelle Zahlen \(\mathbb{R}\)
| Merkmal | Detail |
|---|---|
| Definition | Die Menge aller Zahlen, die auf der Zahlengerade liegen. Dazu gehören sämtliche rationale Zahlen sowie irrationale Zahlen (wie \(\sqrt{2},\pi, e\)). |
| Symbolische Darstellung | \(\mathbb{R}\) |
| Beispiele | \(0, 1, –5, 2, \pi, 3, 1,41421356…\) |
| Eigenschaften | Vollständig: Jede Cauchy‑Folge konvergiert zu einer reellen Zahl. Unendliche Anzahl von Elementen – unzählbar (im Gegensatz zu \(\mathbb{Q}\), das abzählbar ist). Rechenregeln: Addition, Subtraktion, Multiplikation, Division (außer durch 0) bleiben in \(\mathbb{R}\). |
| Besonderheiten | Im Dezimalformat lassen sich reelle Zahlen entweder als endliche, periodische oder nicht periodische (irrationale) Brüche darstellen. Reelle Zahlen bilden die Basis für die Analysis (Grenzwerte, Ableitungen, Integrale). |
| Anwendungsgebiete | Physik, Ingenieurwesen, Wirtschaft – überall dort, wo kontinuierliche Größen modelliert werden. |
Komplexe Zahlen \(\mathbb{C}\)
Der vollständigkeitshalber führe ich hier auch die Menge der komplexen Zahlen an. Diese werdet ihr aber normalerweise – bis auf ein paar Sonderfälle – nicht brauchen.
| Merkmal | Detail |
|---|---|
| Definition | Alle Zahlen der Form \(a+bi\), wobei \(a,b \in \mathbb{R}\) und \(i\) die imaginäre Einheit ist, definiert durch \(i^2=−1\). |
| Symbolische Darstellung | \(\mathbb{C}\) |
| Beispiele | \(3+4i, −2i, 5 \text{ (als 5+0i) }, −1 \text{ (als 0+1i) }\) |
| Eigenschaften | Rechenregeln: Addition, Subtraktion, Multiplikation, Division (außer durch 0) bleiben in \(\mathbb{C}\) . Komplexe Zahlen bilden einen Vektorraum über \(\mathbb{R}\) . |
| Besonderheiten | Die komplexe Ebene (Argand‑Diagramm) visualisiert \(\mathbb{C}\) als zweidimensionales Koordinatensystem. Jede quadratische Gleichung hat in \(\mathbb{C}\) immer zwei Lösungen (Fundamentalsatz der Algebra). |
| Anwendungsgebiete | Signalverarbeitung, Quantenmechanik, Elektrotechnik, komplexe Analysis. |