Halbleiter
Halbleiter sind Stoffe, deren elektrische Leitfähigkeit zwischen der von Leitern (z. B. Metallen) und Nichtleitern (Isolatoren) liegt. Die Leitfähigkeit von Halbleitern ist temperatur- und lichtabhängig. Ein typisches Beispiel ist Silicium (Si), das in der Mikroelektronik weit verbreitet ist. Daraus lassen sich beispielsweise nicht‑lineare Widerstände wie NTCs fertigen.
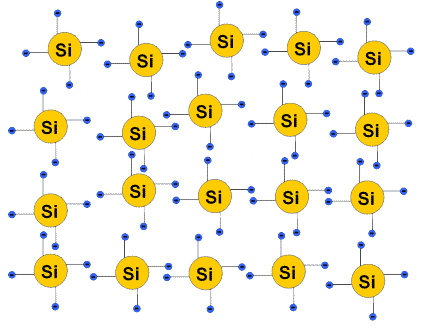
Das Kristallgittermodell
Im Kristallgittermodell wird angenommen, dass die Atome des Halbleiters regelmäßig angeordnet sind. Jedes Atom ist dabei fest im Gitter eingebaut und durch Bindungen mit seinen Nachbaratomen verbunden.
Beispiel: Silicium
- Silicium gehört zur Gruppe IV des Periodensystems → 4 Valenzelektronen in der äußersten Schale.
- Jedes Siliciumatom bildet vier kovalente Bindungen mit den Nachbaratomen.
- So entsteht ein dreidimensionales Kristallgitter.
🌡️Wärme- / 🔆Lichtzufuhr
In einem idealen, reinen Siliciumkristall bei \(0\) K sind alle Valenzelektronen paarweise in Bindungen gebunden. Somit gibt es in diesem Idealfall keine freien Elektronen. Das bedeutet wiederum, dass das Material auch keine elektrische Leitfähigkeit bei dieser Temperatur besitzt.
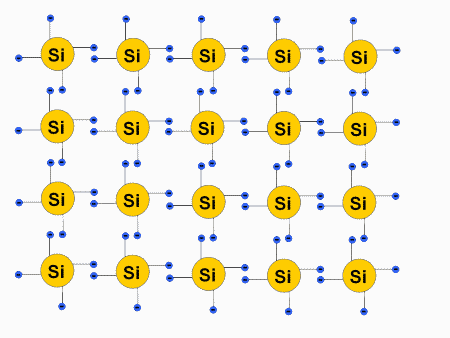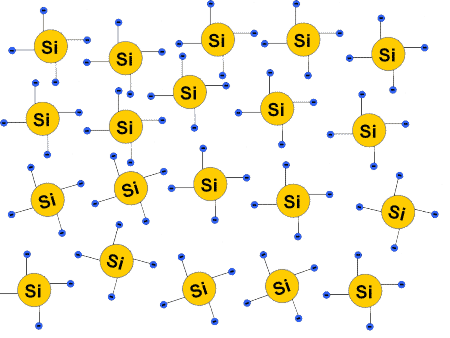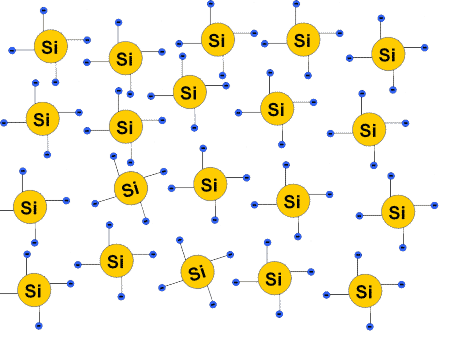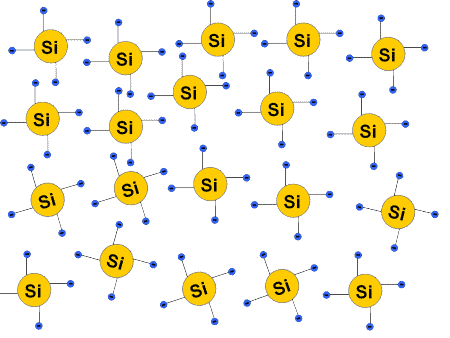
Wenn die Temperatur steigt oder Licht auf den Kristall fällt treten folgende Effekte auf:
- Die Atomrümpfe fangen an zu schwingen, bis die Bindungen ggf. aufgebrochen werden.
- Durch die aufgebrochenen Bindungen werden freie Elektronen erzeugt.
- Das Elektron hinterlässt ein Loch (fehlendes Elektron in einer Bindung).
- Elektronen und Löcher können sich bewegen und somit einen Strom leiten.
Das Bändermodell
Im Bändermodell geht es darum, wie die Elektronen in einem Halbleiter verteilt sind. Die Atome im Kristallgitter erzeugen wiederkehrende „Wellen“ im elektrischen Potential.
Diese Wellen lassen die Elektronen nur in bestimmten Energie‑“Paketen” (Bänder) liegen. Zwischen den Bändern gibt es eine Bandlücke – einen Bereich, in dem keine Elektronenenergie vorhanden ist.
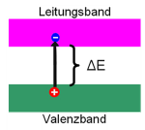
- Valenzband – das höchste vollständig besetzte Band. Alle Elektronen in diesem Band sind in Bindungen mit den Atomen gebunden.
- Leitungsband – das nächsthöhere Band, das bei genügend Energie (z. B. durch Temperatur, Licht oder Dotierung) freier Elektronen enthält.
- Bandlücke \(\Delta E\) – die Energie, die ein Elektron übersteigen muss, um vom Valenzband in das Leitungsband zu gelangen. Für reine Silicium beträgt \(\Delta E\) etwa 1,1 eV bei Raumtemperatur.
Bei \(0\) K sind alle Elektronen im Valenzband und das Leitungsband leer → keine Leitfähigkeit. Sobald jedoch Energie (z. B. Wärme, Licht oder Dotierung) zugeführt wird, können Elektronen die Bandlücke überwinden, ein Elektronen‑Löcher‑Paar entsteht und sich im Leitungsband bzw. im Valenzband bewegen.
Dotierungen
Durch Dotierung werden Fremdatome (z. B. Phosphor oder Bor) in das Gitter eingefügt, die die Bandlücke verzerren und zusätzliche Zustände in das Leitungsband (n‑Dotierung) bzw. in das Valenzband (p‑Dotierung) einbringen. Dadurch wird die Anzahl der freien Ladungsträger erhöht und die Leitfähigkeit gesteigert.
📊 Vergleich: Leiter – Halbleiter – Isolator
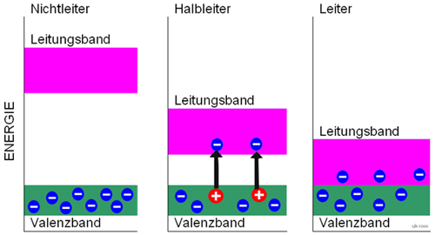
| Material | Bandlücke \(E_g\) in eV | Leitfähigkeit |
|---|---|---|
| Leiter | \( \approx 0 \) | sehr hoch |
| Halbleiter | \( \approx 1 \) | mittel |
| Isolator | \( > 3 \) | sehr niedrig |
💡 Fazit
Das Kristallgittermodell zeigt, dass die besonderen elektrischen Eigenschaften von Halbleitern aus ihrer regelmäßigen Atomstruktur und den kovalenten Bindungen resultieren. Durch gezielte Beeinflussung dieser Bindungen – etwa mit Temperatur, Licht oder Dotierung – kann man die Leitfähigkeit steuern und damit Halbleiter zu den zentralen Materialien moderner Elektronik machen.
Das Bändermodell ergänzt diese Sicht, indem es erklärt, dass die Elektronen in einem Halbleiter nicht beliebig verteilt sind, sondern sich in diskreten Energieniveaus (Bänder) organisieren. Nur wenn Elektronen genügend Energie \(\Delta E\) aufnehmen, um die Bandlücke zu überwinden, gelangen sie in ein Leitungsband und können Strom leiten. Somit verbindet das Bändermodell die atomare Struktur mit dem makroskopischen Verhalten der Leitfähigkeit und liefert die Grundlage für das Design von Transistoren, Solarzellen, NTCs, LDRs und vielen anderen Halbleiterbauelementen.
- www.ulfkonrad.de/physik/9-10/elekt2/halbleiter ↩︎
- www.ulfkonrad.de/physik/9-10/elekt2/halbleiter ↩︎
- Weber, R.: Physik, Teil I: Klassische Physik – Experimentelle und theoretischeGrundlagen. Vieweg+Teubner Verlag Wiesbaden, 2012. ↩︎
- Weber, R.: Physik, Teil I: Klassische Physik – Experimentelle und theoretischeGrundlagen. Vieweg+Teubner Verlag Wiesbaden, 2012. ↩︎