Lineare Funktion aus zwei Punkten aufstellen
In diesem Beitrag lernst du, wie aus zwei gegebenen Punkten \(P_1(x_1,y_1)\) und \(P_2(x_2,y_2)\) die zugehörige lineare Funktion bestimmt wird.
Ansatz
Um eine Funktionsgleichung aufzustellen, muss immer zunächst ein Ansatz aufgestellt werden. Da hier eine lineare Funktion bestimmt werden soll, nehmen wir den Ansatz einer Geraden:
\[ y=mx+b \]1. Schritt: Steigung \(m\) bestimmen
Die Steigung der Geraden ist der Quotient aus der Änderung von \(y\) und der Änderung von \(x\):
\[ m = \frac{\Delta y}{\Delta x} = \frac{y_2 – y_1}{x_2 – x_1} \]In diese Gleichung können die gegebenen Werte der Punkte eingesetzt werden.
2. Schritt: \(y\)-Achsenabschnitt \(b\) bestimmen
Der \(y\)-Achsenabschnitt kann bestimmt werden, indem einer der beiden gegebenen Punkte in den Ansatz der linearen Funktion eingesetzt und nach \(b\) aufgelöst wird:
\[ \begin{align*} y_1 &= m \cdot x_1 + b \\ b &= y_1 – m \cdot x_1 \end{align*} \]3. Schritt: \(m\) und \(b\) in den Ansatz einsetzen
Die gesuchte lineare Funktionsgleichung lautet
\[ y = m \cdot x + b. \]Beispiel:
Gegeben sind die beiden Punkte \(P_1(2, 3)\) und \(P_2(5, 9)\) wodurch eine lineare Funktion verlaufen soll.
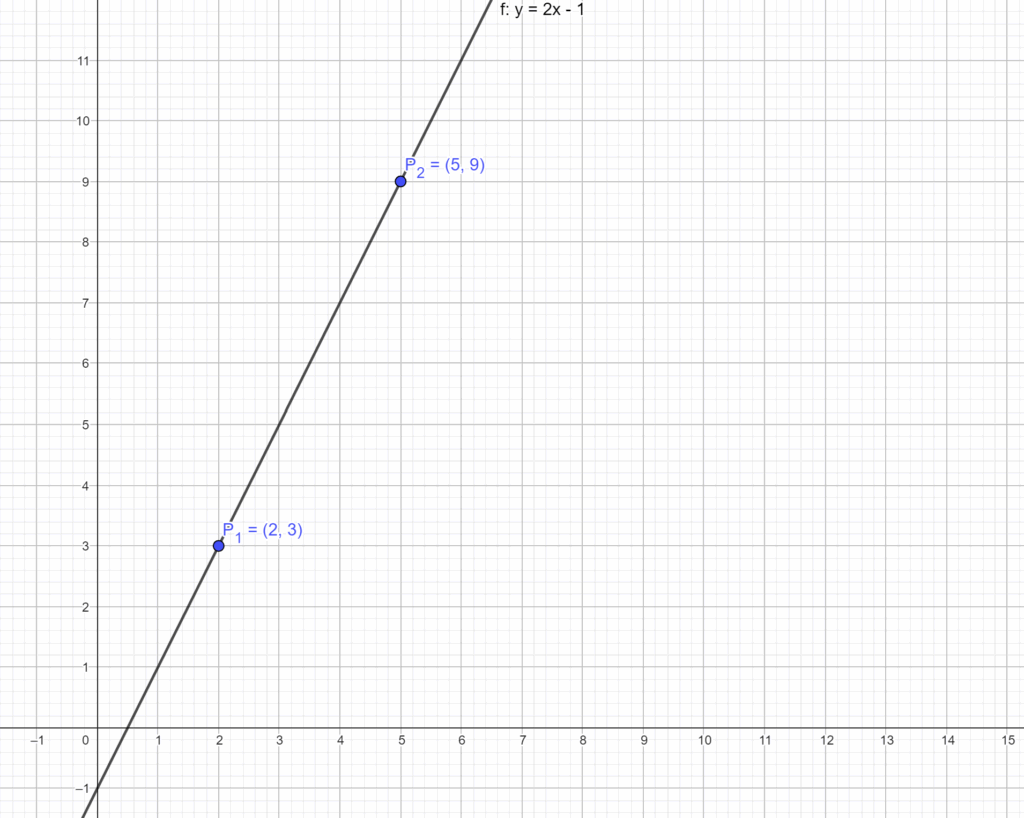
1. Steigung \(m\) bestimmen
Hierfür setzen wir die Werte \(x_1 = 2\) & \(y_1 = 3\) des ersten Punktes und \(x_2 = 5\) & \(y_2 = 9\) des zweiten Punktes in die Gleichung der Steigung ein:
\[ \begin{align*} m &= \frac{y_2 – y_1}{x_2 – x_1} \\ &= \frac{9-3}{5-2} \\ &= \frac{6}{3} = 2 \end{align*} \]Somit beträgt die Steigung \(m = 2\).
2. \(y\)-Achsenabschnitt bestimmen
Hierfür wird die Steigung \(m = 2\) und einer der beiden Punkte in den Ansatz eingesetzt und die Gleichung nach \(b\) umgestellt. In diesem Fallen nehmen wir die Werte aus dem Punkt \(P_1\):
\[ \begin{align*} y_1 &= m \cdot x_1 + b \\ 3 &= 2 \cdot 2 + b \\ 3 &= 4 + b && |-4 \\ b &= -1 \end{align*} \]3. Funktionsgleichung aufstellen
Die bestimmten Werte für \(m\) und \(b\) werden in den Ansatz eingesetzt. Somit lautet die gesuchte lineare Funktion
\[ y = 2x -1. \]