Schnittpunkt(e) zweier Funktionen bestimmen

Ein Schnittpunkt zweier Funktionen ist der Punkt \((SP)\), an dem sich die Graphen der beiden Funktionen im Koordinatensystem schneiden. Dabei haben beide Funktionen denselben \(x\)- und \(y\)-Wert.

Wie bestimmt man einen Schnittpunkt?

1. Setze die beiden Funktionsgleichungen gleich: \(f(x)=g(x)\).
2. Löse die Gleichung nach \(x\) auf.
3. Setze den gefundenen \(x\)-Wert in eine der beiden Funktionen ein, um \(y\) zu bestimmen.
4. Der Schnittpunkt ist dann \((x∣y)\).

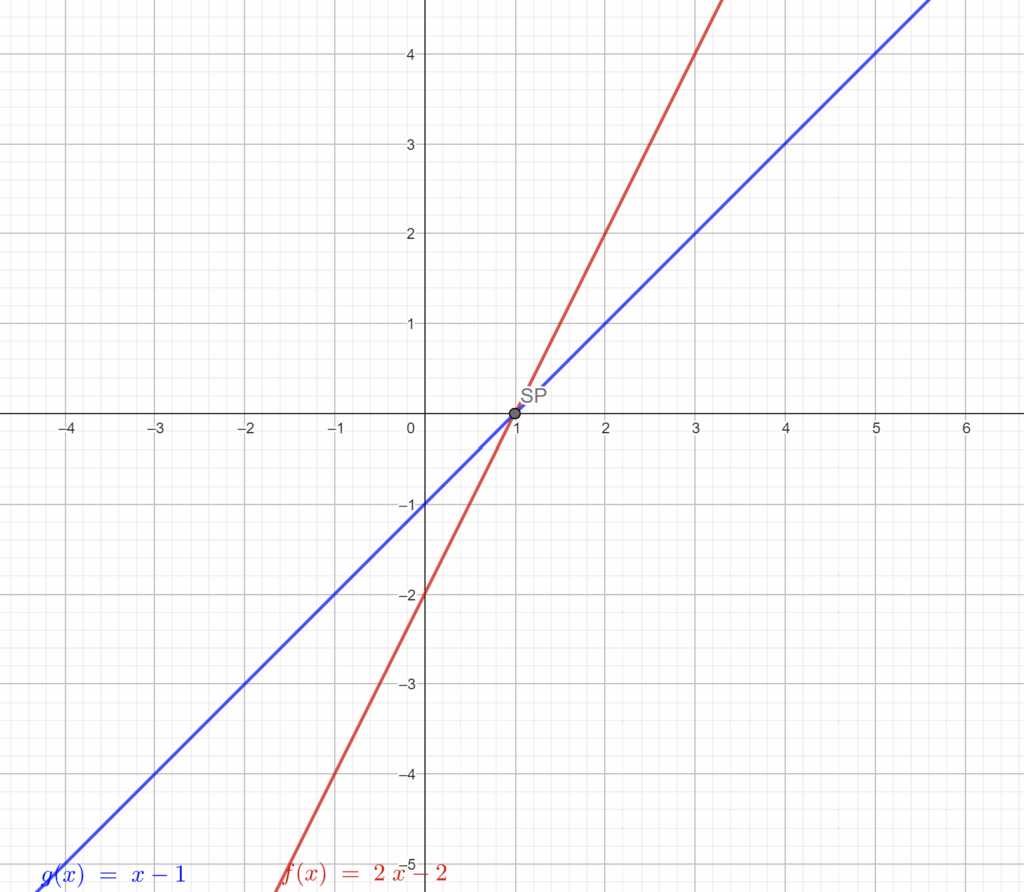
Beispiel

Gegeben sind die beiden linearen Funktionen aus der Abbildung:

\[ f(x) = 2x – 2, \quad g(x) = x – 1 \]

Schritt 1: Gleichsetzen

Setze die beiden Funktionsgleichungen gleich: \(f(x)=g(x)\).

\[ 2x – 2 = x – 1 \]

Schritt 2: Nach \(x\) auflösen

Löse die Gleichung nach \(x\) auf.

\[ \begin{align*} 2x – 2 &= x – 1 && |-x \\ 2x – x – 2 &= x – x -1 \\ x – 2 &= -1 && |+2\\ x &= 1 \end{align*} \]

Schritt 3: \(y\)-Wert bestimmen

Setze den gefundenen \(x\)-Wert in eine der beiden Funktionen ein, um \(y\) zu bestimmen.

\[ y = f(1) = 2\cdot 1 – 2 = 0 \quad \text{oder} \quad y = g(1) = 1-1 = 0 \]

Schritt 4: Schnittpunkt angeben

Der Schnittpunkt ist

\[ SP = (1|0). \]

Übungsaufgaben