Graphisches Differenzieren
Das graphische Differenzieren (graphisches Ableiten) ist eine Methode, um aus dem Graphen einer Funktion den Verlauf ihrer Ableitung abzulesen – ganz ohne Rechnerei.
Dabei schaust du dir die Steigung der Kurve an jeder Stelle an und überträgst diese als neue Funktionswerte in ein eigenes Steigungsdiagramm.
So kannst du herausfinden, wo die Ableitung positiv, negativ oder null ist, und wie stark die Steigung sich ändert.
Das ist besonders nützlich, um das Verhalten einer Funktion besser zu verstehen und wichtige Punkte wie Hoch- und Tiefpunkte oder Wendestellen zu erkennen.
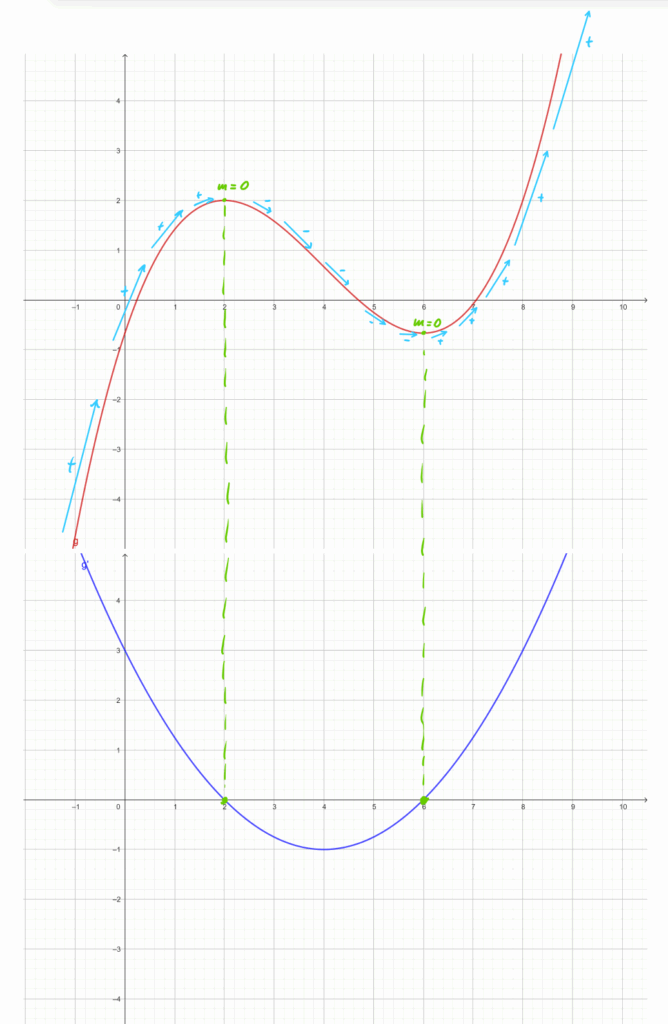
Schritt 1
Punkte des Graphen mit den Stellen bestimmen, wo die Steigung (Änderung) null ist und Stellen im Änderungsgraphen markieren.
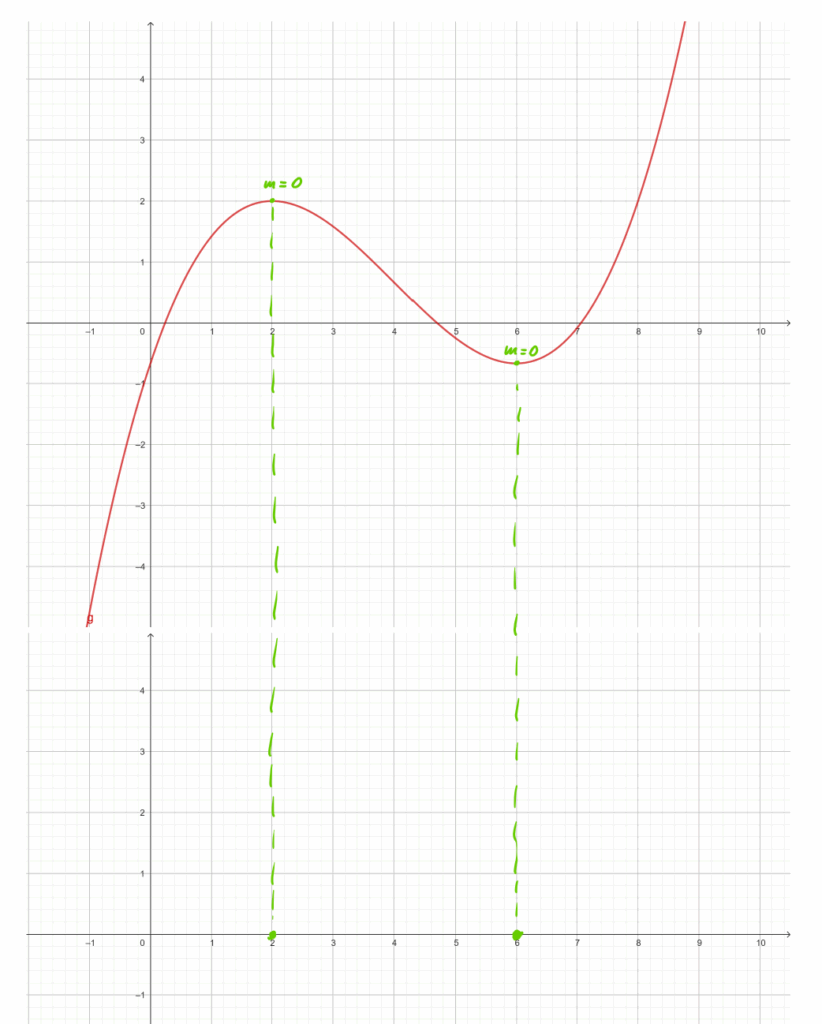
Schritt 2
Intervalle bestimmen, in denen die Änderung nur positiv ((+)) oder nur negativ ((-)) ist, und diese im Änderungsgraphen markieren.
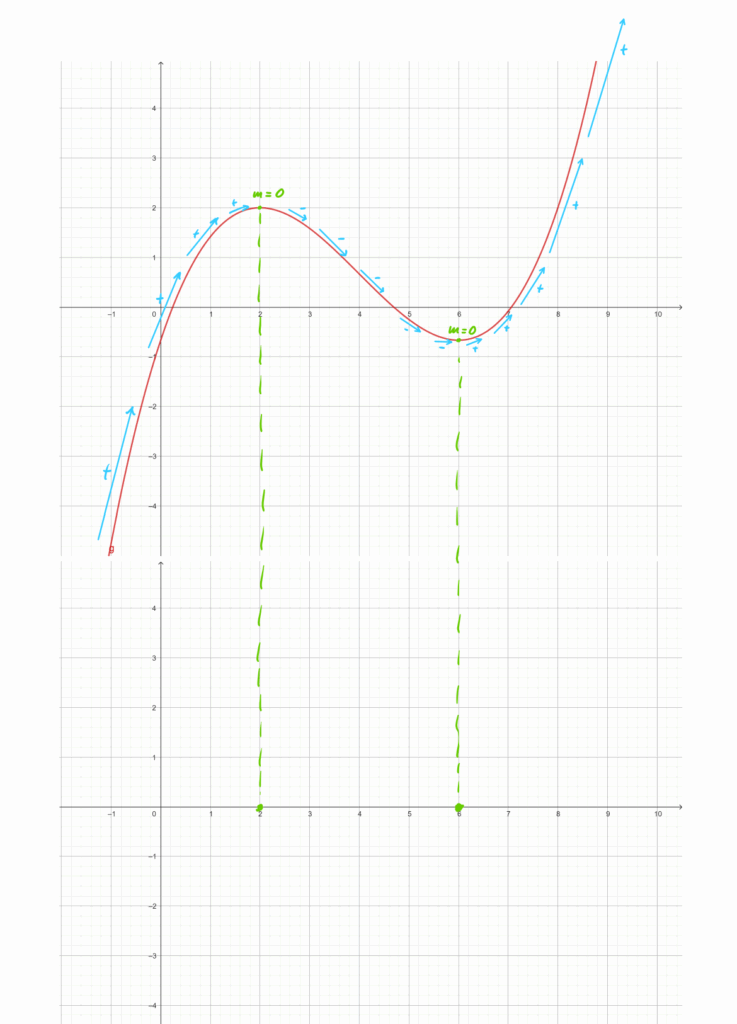
Schritt 3
Punkte mit maximaler/minimaler Änderung bestimmen und im Änderungsgraphen markieren.