Potenzgesetze

Eine Potenz ist eine Kurzschreibweise für eine wiederholte Multiplikation.
Sie besteht aus der Basis und dem Exponent.

\[ {\underbrace{a}_{\text{Basis}}}^n = \underbrace{a \cdot a \cdot \dots \cdot a}_{n\text{ mal}} \]

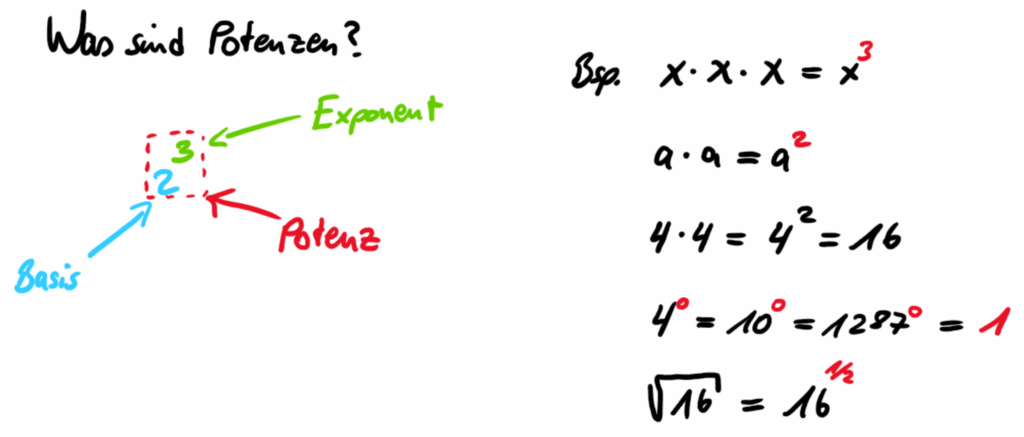
• Basis \(a\): Die Zahl, die mehrfach mit sich selbst multipliziert wird.
• Exponent \(n\): Gibt an, wie oft die Basis mit sich selbst multipliziert wird.

Beispiel:

\[ 2^4 = 2 \cdot 2 \cdot 2 \cdot 2 = 16 \]

In diesem Beitrag findest du eine kompakte Zusammenfassung der wichtigsten Potenzgesetze mit Beispielen. Die Regeln gelten für alle reellen Zahlen \(a, b\) (mit \(a \ne b\)) und natürliche Zahlen \(m,n\).

Multiplikation mit gleicher Basis

Regel: Wenn zwei Potenzen mit gleicher Basis multipliziert werden, addieren sich die Exponenten:

\[ a^m \cdot a^n = a^{m+n} \]

Beispiel:

\[ 3^4 \cdot 3^2 = 3^{4+2} = 3^6 \]

Division mit gleicher Basis

Regel: Exponenten werden subtrahiert.

\[ \frac{a^m}{a^n} = a^{m-n} \]

Beispiel:

\[ \frac{5^6}{5^2} = 5^{6-2} = 5^4 \]

Potenz einer Potenz

Regel: Exponenten werden multipliziert.

\[ (a^m)^n = a^{m \cdot n} \]

Beispiel:

\[ (2^3)^4 = 2^{3 \cdot 4} = 2^{12} \]

Potenz eines Produkts

Regel: Jeder Faktor wird einzeln potenziert.

\[ (a \cdot b)^n = a^n \cdot b^n \]

Beispiel:

\[ (2 \cdot 3)^4 = 2^4 \cdot 3^4 = 16 \cdot 81 \]

Potenz eines Quotienten

Regel: Zähler und Nenner werden einzeln potenziert.

\[ \left( \frac{a}{b} \right)^n = \frac{a^n}{b^n} \]

Beispiel:

\[ \left( \frac{3}{5} \right)^2 = \frac{3^2}{5^2} = \frac{9}{25} \]

Nullter Exponent

Regel: Jede Zahl (außer 0) hoch 0 ergibt 1.

\[ a^0 = 1 \quad \text{für } a \ne 0 \]

Beispiel:

\[ 7^0 = 1 \]

Negativer Exponent

Regel: Aus der Potenz wird ein Bruch.

\[ a^{-n} = \frac{1}{a^n} \]

Beispiel:

\[ 2^{-3} = \frac{1}{2^3} = \frac{1}{8} \]