Herleitung der lokalen Änderungsrate mittels h-Methode

Dieser Beitrag wird gerade erstellt und ist damit noch nicht vollständig!
In diesem Beitrag geht es um die Herleitung der h‑Methode, also um die Bestimmung der lokalen Änderungsrate an einem einzigen Punkt einer Funktion. Wenn du nicht an der Herleitung interessiert bist und nur ein Rechenbeispiel suchst, dann klicke hier.
Wiederholung: durschnittliche Änderungsrate
Bevor wir in die h‑Methode einsteigen, erinnern wir uns zunächst an die durchschnittliche Änderungsrate. Sie beschreibt die Steigung einer Sekante zwischen zwei Punkten \(A\) und \(B\) auf einer Kurve und ist damit das Vorwissen, das wir für die h‑Methode benötigen.
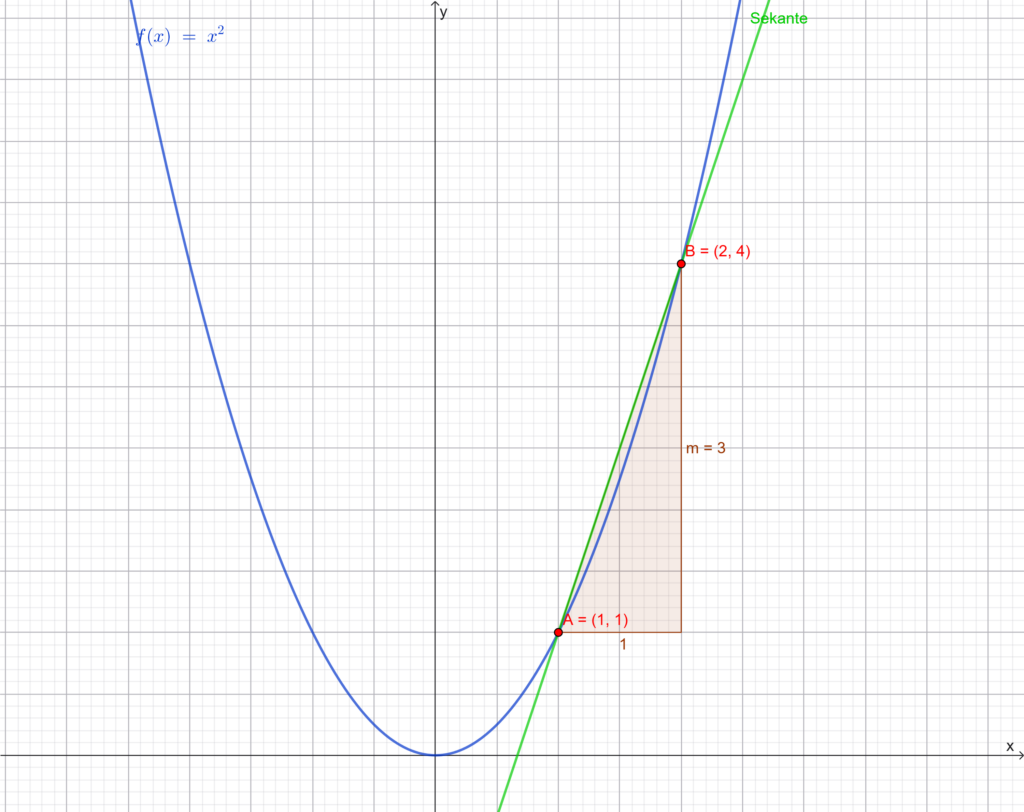
In dem Beitrag zur durchschnittlichen Änderungsrate haben wir diese anhand der Funktion \(f(x)=x^2\) zwischen den beiden Punkte \(A(1|1)\) und \(B(2|4)\) mit Hilfe des bestimmt Differenzenquotienten bestimmt:
\[ m_{[a,b]} = \frac{f(b)-f(a)}{b-a} \]Setzt man die Koordinaten von A und B ein, erhält man
\[ m_{[1,2]} = \frac{f(2)-f(1)}{2-1} = \frac{4-1}{1} = 3. \]Damit haben wir die Steigung der Sekante zwischen den Punkten \(A\) und \(B\) bestimmt. Nun wollen wir jedoch die Steigung an exakt dem Punkt \(A\), also die lokale Änderungsrate, bestimmen.
Herleitung der durschnittlichen Änderungsrate
Die erste Idee wäre, den Punkt \(B\) exakt auf den Punkt \(A\) zu legen, also \( B(1|1) \). Dann wäre der Differenzenquotient
\[ m_{[1,1]} = \frac{f(1)-f(1)}{1-1} = \frac{0}{0}. \]Da der Nenner Null wird, ergibt sich ein undefinierter Ausdruck, der in der Praxis als Null interpretiert werden würde. Dies macht keinen Sinn, denn die Tangente an der Stelle \( x=1 \) hat eine Steigung größer als Null, wie die graphische Darstellung zeigt.
Da der Nenner Null wird, ergibt sich ein undefinierter Ausdruck, der in der Praxis als Null interpretiert werden würde. Dies macht keinen Sinn, denn die Tangente an der Stelle \( x=1 \) hat eine Steigung größer als Null, wie die graphische Darstellung zeigt.
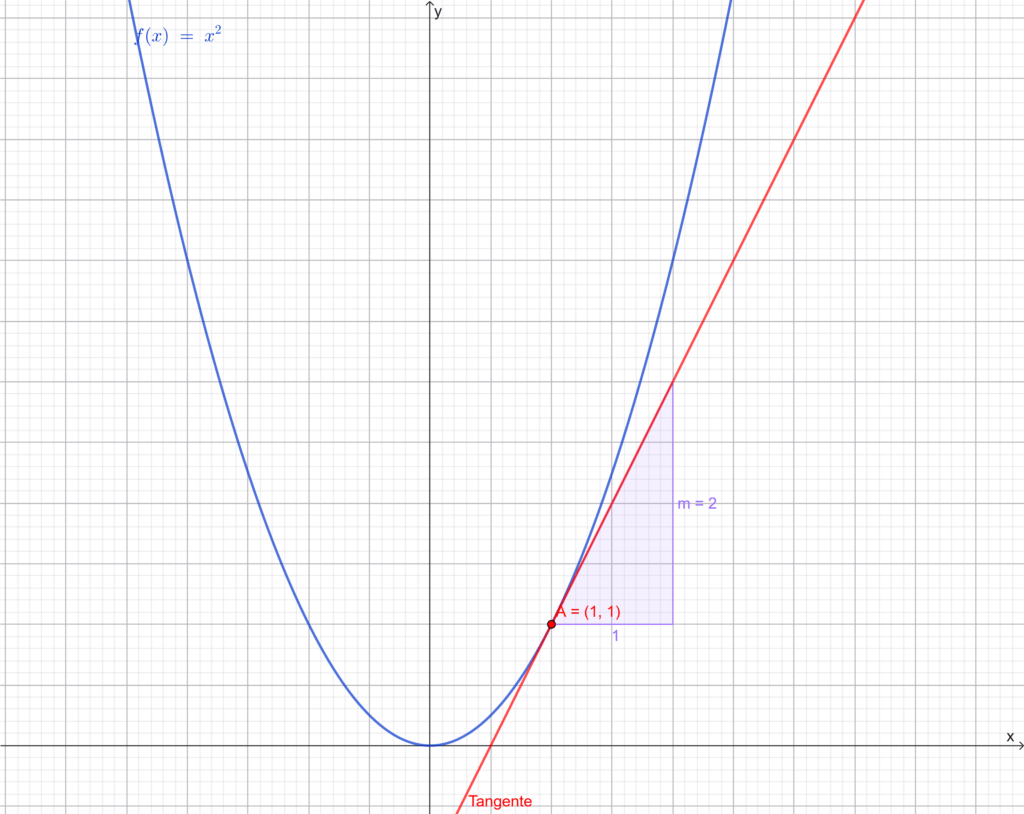
Die zweite Idee besteht darin, \(B\) nicht exakt auf \(A\) zu platzieren, sondern sehr nahe an \(A\).
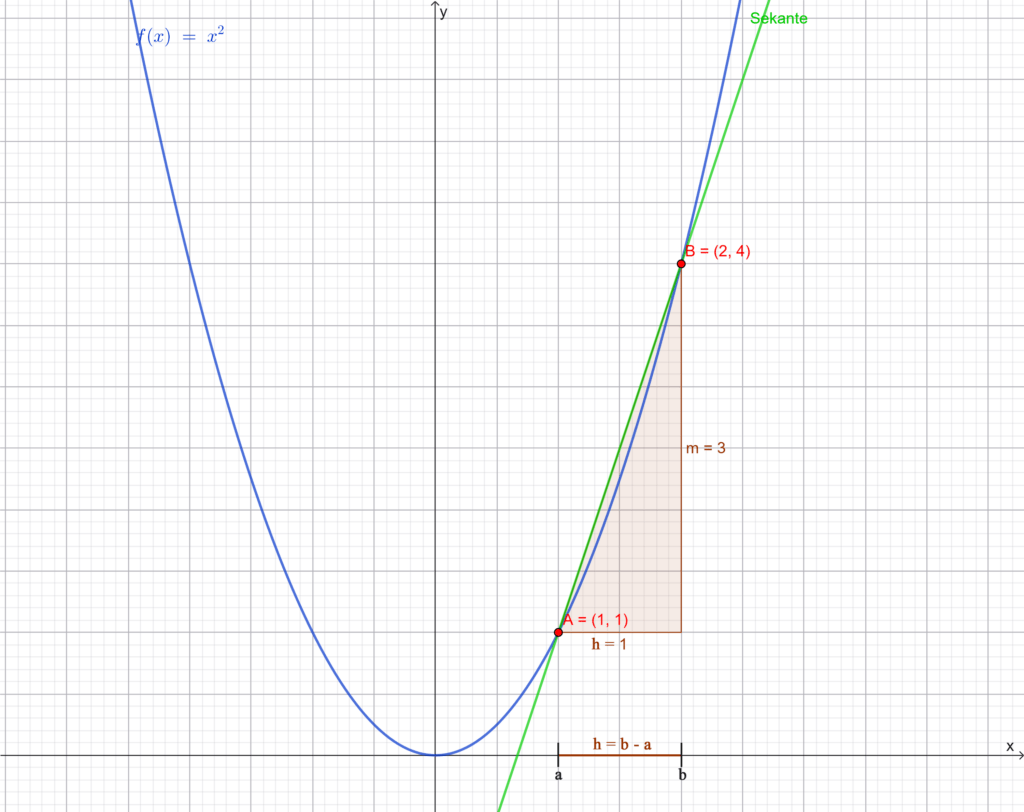
Wir wählen also den zweiten Punkt \( B \) auf der Kurve, der nicht exakt auf \( A \) liegt, sondern nur einen kleinen horizontalen Abstand \( h \) von \( A \) entfernt ist. Beispielsweise setzen wir für \( B \) die Koordinaten \( B(1,1 \mid f(1,1)) \). Hierbei ist \( h = b – a \).
Wenn wir mit diesen neuen Werten den Differenzenquotienten berechnen, dann bekommen wir
\[ m = \frac{f(1,1)-f(1)}{1,1-1} = 2,1. \]Da der Punkt \( B \) nicht exakt auf \( A \) liegt, und somit der horizontale Abstand \( h = 1,1 – 1 \neq 0\) ist, handelt es sich bei unserem Ergebnis von \(m = 2,1 \) um nur ein ungefähres Ergebnis. Um die Genauigkeit zu erhöhen, verkleinern wir \( h \) weiter. Du kannst Wir stellen die Werte für verschiedene ( h ) in einer Tabelle zusammen:
Die Tabelle und die Animation zeigen deutlich, dass der Differenzenquotient mit sinkendem \( h \) immer näher an den Wert \(m = 2 \) herankommt. Hierbei handelt es sich um ein Grenzwertverhalten.
Das Konzept des Grenzwerts liefert uns die exakte lokale Änderungsrate: