Das Gaußverfahren (Matrixschreibweise)

Das Gaußverfahren wird zum Lösen von linearen Gleichungssystemen verwendet. In diesem Beitrag wird der Gaußalgorithmus anhand eines zunächst einfachen Beispiels erklärt.

Zunächst wird das lineare Gleichungssystem in die Matrixschreibweise überführt, damit wir uns Schreibarbeit ersparen:

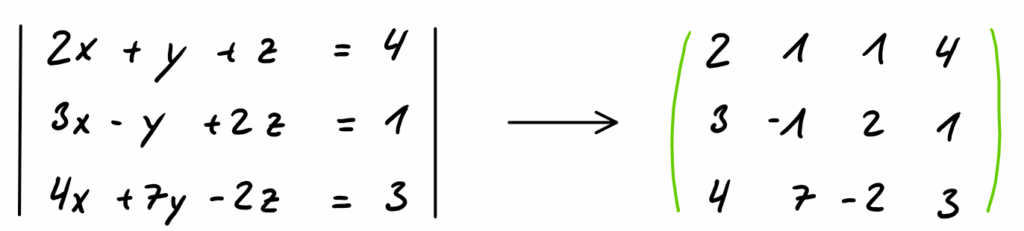
Ziel ist es nun die Einträge der Matrix stufenartig auf Null zu setzen.

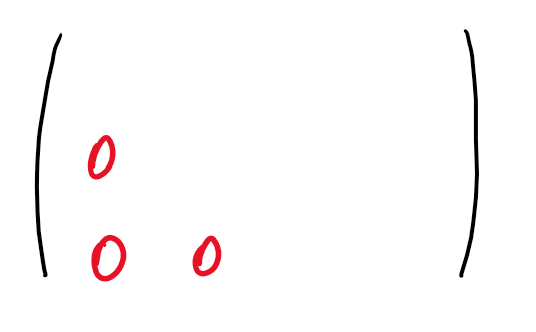
Hierzu schauen wir uns zunächst die ersten beiden Zeilen an und überlegen, wie diese so verändert werden können, damit bei einer Addition der erste Eintrag der zweiten Zeile Null wird.

\begin{align} 2 \cdot (-3)+3 \cdot 2 =& \text{ }0 \\ -6 + 6 =& \text{ }0 \end{align}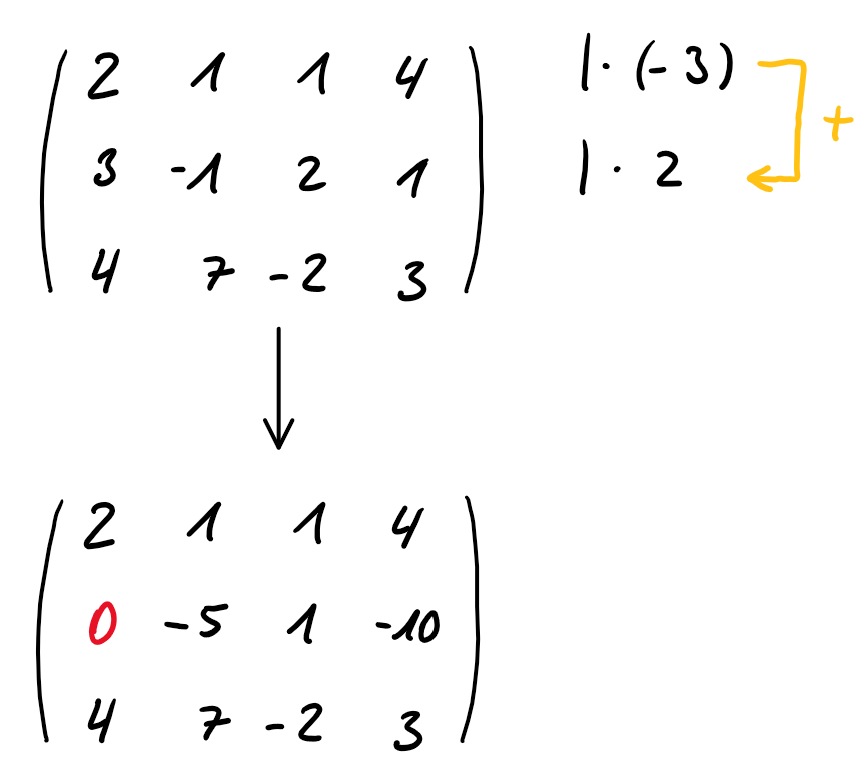

Nun wird die zweite und die dritte Zeile betrachtet und so verändert, dass bei einer Addition der erste Eintrag der dritten Zeile Null wird.

\begin{align} 2 \cdot (-2) + 4 =& \text{ }0\\ -4 + 4 =& \text{ }0 \end{align}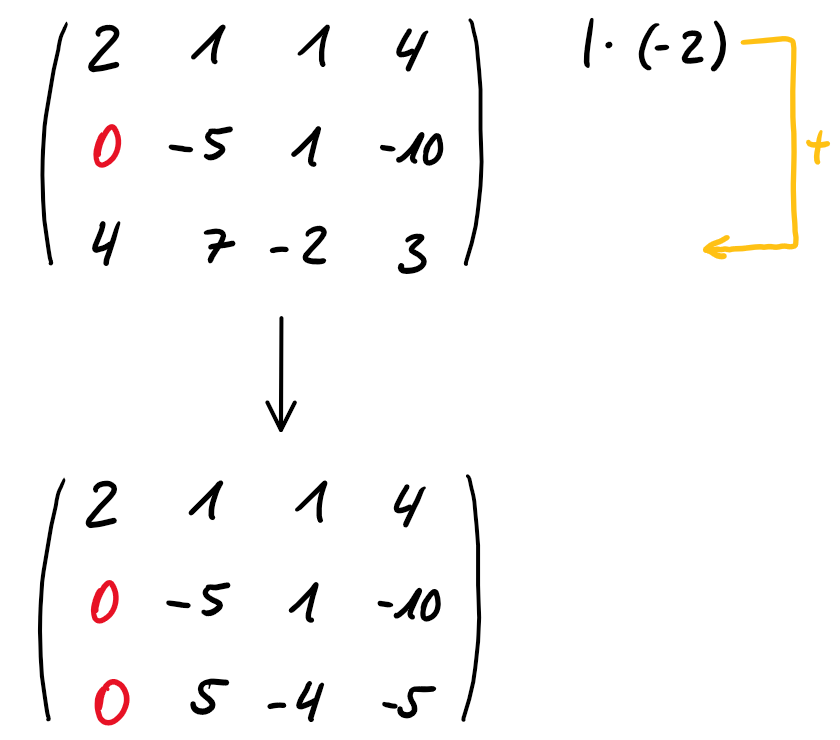

Da wir bei einem dreizeiligem Gleichungssystem nun bereits in der letzten Zeile angekommen sind, wird versucht den zweiten Eintrag der letzten Zeile Null zu bekommen.

Nun werden die letzten beiden Zeilen wie zuvor dementsprechend umgebaut, damit sie bei der Addition von vorletzter und letzter Zeile den ersten und zweiten Eintrag der letzten Zeile Null ergibt.

\[ -5 + 5 = 0 \]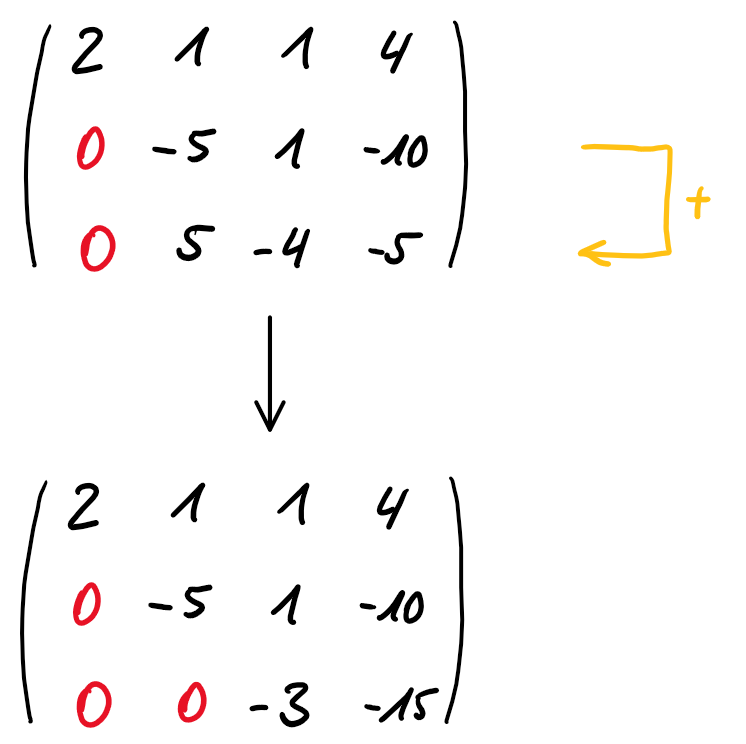

Wenn die Matrix stufenartig Null (von unten links ausgehend) aufgebaut ist, ist der Gaußalgorithmus beendet und die Matrix kann wieder in die normale Schreibweise überführt werden:

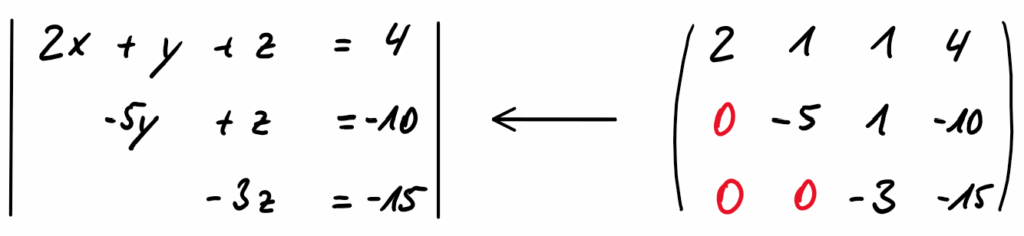
Dieses vereinfachte Gleichungssystem kann nun von unten nach oben durch Umstellen der Gleichung und anschließendem Einsetzen in die darüberliegende Gleichung recht schnell gelöst werden.